Basic Idea:
I want to show you what an DDFS is, how it works and how to implement it on an FPGA.
Imagine you want to create a Sinusoid at a DAC. The DAC is accepting a digital value and will convert it to a analogue value. If there are multiple values in a periodic manner we say its a signal, a signal is a periodic flow of values.
If we want to create a sinusoid signal we therefore need to send the discrete values of the sinusoid to the ADC.
Lets say our DAC is working with 10MHz, which means that it will generate a analogue value every 0,1µs (1/10MHz).
We want to create a sinus with a frequency of 1,25MHz. Which means that we will have to send 8 values per cycle to the DAC in order to meet the 10MHz of the DAC.
We now need to get those 8 values. We need to split one cycle of our desired signal (sinus) into 10 equally distributed values.
-1<x<8
which will give us
0 0
1 0,707106781
2 1
3 0,707106781
4 0
5 -0,707106781
6 -1
7 -0,707106781
If you plot those values you already can imagine what it is:
All we do need to do know is to cycle through the values and send the corresponding value every 0,1µs
Implementation
Because the cycling etc would be very expensive on a microcontroller this structure is usually build in hardware/FPGA.
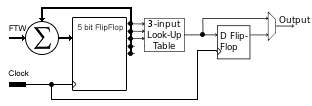
Our list with the values is stored in a Look up table (LUT) which is SRAM on a FPGA and ROM on an ASIC.
We do know how many entries we need, 8. How many bits do we need to address that?
so log(8)/log(2)=3 bit.
We end up with something like this:

We do have 3 address lines to address the entry we want to load.
So if the adress is 010b (2d) the output will be 1, 101b (5d) will give -0,707106781.
please note that there is a FlipFlop to make sure our output is synchronous with the clock. The clock in our case would have to be set to 10MHz to by synchronous with the DAC.
Next thing we need to do is to make the address cycle from 0 to 7.
How to do it?
Just thing of programming in c++ (for example)
int count=0;
while (true)
{
count=++count%8;
cout<<“value: “<<count<<endl;
}
this will give us:
value: 0
value: 1
value: 2
value: 3
value: 4
value: 5
value: 6
value: 7
value: 0
value: 1
value: 2
value: 3
…
and it will do so forever. This is the signal we do need. It will address our entries in the LUT one after another and send the discrete sinus to the DAC.
If you plot this signal you well see that:
this is a sawtooth signal.
To generate this signal we need a FlipFlop which is triggered by a clock and on every cycle its value is incremented by 1. It will overflow if the maximum value of the FlipFlop is reached and start from 0 again.
That is the basic structure of an DDFS.
The problem with it is that everything is fixed there, the frequency, the amplitude and the phase shift.
Frequency control
The trick on how to change the frequency is to change the frequency of the address signal (sawtooth).
Remember that inside the address generator we used the previous values and incremented it by 1 every cycle. But what happens if we increment it by 2 every cycle?
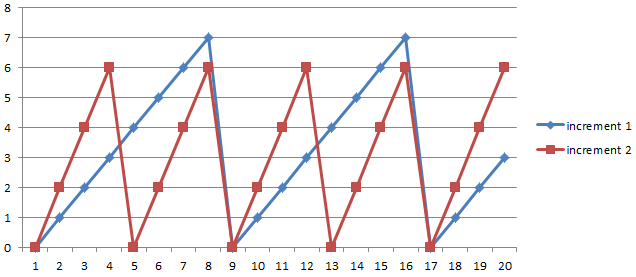
The frequency of the sawtooth signal will double and therefore also the frequency of the sinus signal. Please note that some of the values within the LUT are skipped now!
Also note that you still need to take the Nyquist Frequency within consideration. As the DAC frequency and the LUT size are limited you can not infinitely increase the frequency.
The value we increment the counter with every cycle is called the “Frequency Tuning Word” FTW.
The method above will allow to set frequencies as multiple of the base frequency (FTW=1) but nothing in between. Fore some applications this is fine, for others its not.
You can solve this issue by introducing fractional bits.
Lets assume we stay with our 3 bit LUT and we want to introduce 2 fractional bits. We can express this using the Q-Format, in Q format this constellation would be Q3.2.
We now do need a 5bit FlipFlop to generate our sawtooth. The trick is that just the non fractional 3 bits of the FlipFlop are used to address the LUT.
Its important that our FTW now need to be in the Q3.2 format too!
Imagine it would be our old 1, so in 5 bits 00001. Then we would need 4 cycles in order to reach the next entry in the LUT. Therefore the output frequency would be be 1/4th of the base frequency.
A few words about fractional bits in a fixed point arithmetic.
in our example we assume that we have 2 fractional bits.
To make a long story short, this is the representation of all 5 bits withing Q3.2, the bits are separated by a semicolon
2^3;2^2,2^1; . 2^-1;2^-2; which is 4;2;1; . 0,5;0,25
lets try it:
01001 is 2+0,25=2,25
this is giving us the possibility to adjust our frequency much more precise!
But there is also a downside. Imagine we half the base frequency, as the DAC is of course still working with its own frequency but is just getting a new value every 2 cycles the signal is distorted:

Amplitude control
In the previous consideration we expected that the LUT will hold values that are equally distributed within the boundaries of the underling bit-width. This bit width is not necessary equal with the bit width of the DAC. Therefore, by placing a multiplicatior we can set the amplitude of the signal.
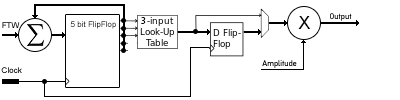
Offset
We can apply an offset by adding a value before we send the signal to the DAC
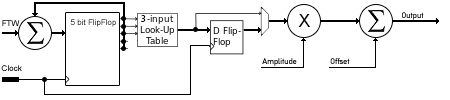
Phase Shift

Using qudrature information
Currently we are storing the whole sinus in the LUT. This isn’t necessary. We also can store just the values from 0 to 1/2pi (or 0° to 90°). And the first 2 bit can be used as quadrature information. Therefore the LUT size can be reduced by 2 bits. Or, we can use the old LUT size to reach a much higher precision, in this case we need 2 more bits for our sawtooth generator.
Our 3 bit LUT can hold 8 values, by interpreting the first 2 bits of the phase word (the signal from the sawtooth to the LUT) we can determine in which quadrature we are.
00
01
10
11
Now we can compare the old output with the new:
old
new
Formulas:
Phase resolution:
The Phase resolution will tell us the step-size between 2 values in the LUT. If we store a whole Sinusoid function within an N-bit LUT, the Phase resolution is
In degree: In radiant:
If we use the quadrature information and store just 1/4 of the cycle the precision is 4 times higher:
In degree: In radiant:
Frequency Tuning Word (FTW)
The FTW is the multiplier for the sawtooth signal generator which will determine its frequency and therefore the frequency of the output. The output frequency is:
where N is the number of phasepoints.
If the whole cycle is stored in the LUT, N is the LUT Size.
If we use quadrature information N is the LUT size*4!
So if we want to have the FTW for a desired target frequency its:
The problem is that we can just meet target frequencies which are a multiple of the clock frequency. Therefore (if we do not use fractional bits) we have to round to the closest integer.
Its obvious that we will have an frequency error at this point if the calculated FTW is not an integer
Therefore we first need to calculate the actual output frequency using
for an absolute error we simply subtract the actual output frequency from our target frequency and get the absolute error
for an relative error we need the ratio between the desired and the actual frequency
Using fractional Bits
As mentioned above we can use fractional bits to reach a higher precision. The only thing we need to do is to calculate the FTW with fractional bits.
Example:
Assume a Q2.4 FTW. So we have 2 bits for the integer and 4 bits for the fractional part. Note that the fractional bits are not used to adress the LUT.
We want a FTW of 1.44 our bitmask is xx.xxx Lets write the whole thing down again vertically
x 2^2 (2)
x 2^1 (1)
.
x 2^-1 (0,5)
x 2^-2 (0,25)
x 2^-3 (0,125)
x 2^-4 (0,0625)
we convert the integer and fractional part separately. For the integer part in this case its simply 01.xxx.
Now we need to convert the fractional part into binary representation. We compare the fractional part with our fractional bits
0,44 > (x2^-1 <0,5>) no, so this bit is 0
0,44 > (x2^-2 <0,25>) yes, so this bit is 1 we now need to subtract the 0,25 from 0,44 which will give 0,19
0,19 > (x2^-3 <0,125>) yes, so this bit is 1 subtract it from 0,19 will give 0,065
0,065> (x2^-4 <0,0625>) yes, so 0,065-0,0625= 0,0025 (our rest)
so we have 01.0111 for the FTW, but if you convert it back (0,25+0,125+0,0625) you will see that this number is 1,4375 which is closer to our desired frequency but still does not meet it exactly.
The frequency error calculation than can be used to determine the error.
DDFS Verilog Implementation
The code below shows a basic DDFS implementation
module ddfs_sin(clk, FTW, q ); input wire clk; input wire [12:0] FTW; output reg [15:0] q; ////////////////////////////////////////////////////7 reg [12:0] cnt; reg [15:0] sine; reg [7:0] index; always@(posedge clk) begin index<=cnt[12:5]; cnt <= cnt + FTW; end ////////////////////////////////////////////////////// always@(posedge clk) begin q<=sine; end always @(index) begin case(index) 0: sine = 16'd0; 1: sine = 16'd807; 2: sine = 16'd1614; 3: sine = 16'd2419; 4: sine = 16'd3224; 5: sine = 16'd4026; 6: sine = 16'd4826; 7: sine = 16'd5623; 8: sine = 16'd6417; 9: sine = 16'd7207; 10: sine = 16'd7992; 11: sine = 16'd8773; 12: sine = 16'd9548; 13: sine = 16'd10317; 14: sine = 16'd11080; 15: sine = 16'd11837; 16: sine = 16'd12586; 17: sine = 16'd13327; 18: sine = 16'd14061; 19: sine = 16'd14786; 20: sine = 16'd15502; 21: sine = 16'd16208; 22: sine = 16'd16905; 23: sine = 16'd17592; 24: sine = 16'd18267; 25: sine = 16'd18932; 26: sine = 16'd19585; 27: sine = 16'd20226; 28: sine = 16'd20855; 29: sine = 16'd21472; 30: sine = 16'd22075; 31: sine = 16'd22665; 32: sine = 16'd23241; 33: sine = 16'd23803; 34: sine = 16'd24351; 35: sine = 16'd24884; 36: sine = 16'd25401; 37: sine = 16'd25904; 38: sine = 16'd26390; 39: sine = 16'd26861; 40: sine = 16'd27315; 41: sine = 16'd27753; 42: sine = 16'd28173; 43: sine = 16'd28577; 44: sine = 16'd28963; 45: sine = 16'd29332; 46: sine = 16'd29683; 47: sine = 16'd30016; 48: sine = 16'd30331; 49: sine = 16'd30627; 50: sine = 16'd30905; 51: sine = 16'd31164; 52: sine = 16'd31404; 53: sine = 16'd31625; 54: sine = 16'd31826; 55: sine = 16'd32009; 56: sine = 16'd32172; 57: sine = 16'd32315; 58: sine = 16'd32439; 59: sine = 16'd32543; 60: sine = 16'd32628; 61: sine = 16'd32692; 62: sine = 16'd32737; 63: sine = 16'd32762; 64: sine = 16'd32767; 65: sine = 16'd32752; 66: sine = 16'd32717; 67: sine = 16'd32662; 68: sine = 16'd32588; 69: sine = 16'd32494; 70: sine = 16'd32380; 71: sine = 16'd32246; 72: sine = 16'd32093; 73: sine = 16'd31920; 74: sine = 16'd31728; 75: sine = 16'd31517; 76: sine = 16'd31286; 77: sine = 16'd31037; 78: sine = 16'd30768; 79: sine = 16'd30481; 80: sine = 16'd30176; 81: sine = 16'd29852; 82: sine = 16'd29510; 83: sine = 16'd29150; 84: sine = 16'd28772; 85: sine = 16'd28377; 86: sine = 16'd27965; 87: sine = 16'd27536; 88: sine = 16'd27090; 89: sine = 16'd26628; 90: sine = 16'd26149; 91: sine = 16'd25654; 92: sine = 16'd25144; 93: sine = 16'd24619; 94: sine = 16'd24079; 95: sine = 16'd23524; 96: sine = 16'd22955; 97: sine = 16'd22372; 98: sine = 16'd21775; 99: sine = 16'd21165; 100: sine = 16'd20543; 101: sine = 16'd19907; 102: sine = 16'd19260; 103: sine = 16'd18601; 104: sine = 16'd17931; 105: sine = 16'd17250; 106: sine = 16'd16558; 107: sine = 16'd15856; 108: sine = 16'd15145; 109: sine = 16'd14424; 110: sine = 16'd13695; 111: sine = 16'd12958; 112: sine = 16'd12212; 113: sine = 16'd11459; 114: sine = 16'd10700; 115: sine = 16'd9933; 116: sine = 16'd9161; 117: sine = 16'd8383; 118: sine = 16'd7600; 119: sine = 16'd6812; 120: sine = 16'd6021; 121: sine = 16'd5225; 122: sine = 16'd4427; 123: sine = 16'd3625; 124: sine = 16'd2822; 125: sine = 16'd2017; 126: sine = 16'd1210; 127: sine = 16'd403; 129: sine = 16'd65133; 130: sine = 16'd64326; 131: sine = 16'd63519; 132: sine = 16'd62714; 133: sine = 16'd61911; 134: sine = 16'd61109; 135: sine = 16'd60311; 136: sine = 16'd59515; 137: sine = 16'd58724; 138: sine = 16'd57936; 139: sine = 16'd57153; 140: sine = 16'd56375; 141: sine = 16'd55603; 142: sine = 16'd54836; 143: sine = 16'd54077; 144: sine = 16'd53324; 145: sine = 16'd52578; 146: sine = 16'd51841; 147: sine = 16'd51112; 148: sine = 16'd50391; 149: sine = 16'd49680; 150: sine = 16'd48978; 151: sine = 16'd48286; 152: sine = 16'd47605; 153: sine = 16'd46935; 154: sine = 16'd46276; 155: sine = 16'd45629; 156: sine = 16'd44993; 157: sine = 16'd44371; 158: sine = 16'd43761; 159: sine = 16'd43164; 160: sine = 16'd42581; 161: sine = 16'd42012; 162: sine = 16'd41457; 163: sine = 16'd40917; 164: sine = 16'd40392; 165: sine = 16'd39882; 166: sine = 16'd39387; 167: sine = 16'd38908; 168: sine = 16'd38446; 169: sine = 16'd38000; 170: sine = 16'd37571; 171: sine = 16'd37159; 172: sine = 16'd36764; 173: sine = 16'd36386; 174: sine = 16'd36026; 175: sine = 16'd35684; 176: sine = 16'd35360; 177: sine = 16'd35055; 178: sine = 16'd34768; 179: sine = 16'd34499; 180: sine = 16'd34250; 181: sine = 16'd34019; 182: sine = 16'd33808; 183: sine = 16'd33616; 184: sine = 16'd33443; 185: sine = 16'd33290; 186: sine = 16'd33156; 187: sine = 16'd33042; 188: sine = 16'd32948; 189: sine = 16'd32874; 190: sine = 16'd32819; 191: sine = 16'd32784; 192: sine = 16'd32769; 193: sine = 16'd32774; 194: sine = 16'd32799; 195: sine = 16'd32844; 196: sine = 16'd32908; 197: sine = 16'd32993; 198: sine = 16'd33097; 199: sine = 16'd33221; 200: sine = 16'd33364; 201: sine = 16'd33527; 202: sine = 16'd33710; 203: sine = 16'd33911; 204: sine = 16'd34132; 205: sine = 16'd34372; 206: sine = 16'd34631; 207: sine = 16'd34909; 208: sine = 16'd35205; 209: sine = 16'd35520; 210: sine = 16'd35853; 211: sine = 16'd36204; 212: sine = 16'd36573; 213: sine = 16'd36959; 214: sine = 16'd37363; 215: sine = 16'd37783; 216: sine = 16'd38221; 217: sine = 16'd38675; 218: sine = 16'd39146; 219: sine = 16'd39632; 220: sine = 16'd40135; 221: sine = 16'd40652; 222: sine = 16'd41185; 223: sine = 16'd41733; 224: sine = 16'd42295; 225: sine = 16'd42871; 226: sine = 16'd43461; 227: sine = 16'd44064; 228: sine = 16'd44681; 229: sine = 16'd45310; 230: sine = 16'd45951; 231: sine = 16'd46604; 232: sine = 16'd47269; 233: sine = 16'd47944; 234: sine = 16'd48631; 235: sine = 16'd49328; 236: sine = 16'd50034; 237: sine = 16'd50750; 238: sine = 16'd51475; 239: sine = 16'd52209; 240: sine = 16'd52950; 241: sine = 16'd53699; 242: sine = 16'd54456; 243: sine = 16'd55219; 244: sine = 16'd55988; 245: sine = 16'd56763; 246: sine = 16'd57544; 247: sine = 16'd58329; 248: sine = 16'd59119; 249: sine = 16'd59913; 250: sine = 16'd60710; 251: sine = 16'd61510; 252: sine = 16'd62312; 253: sine = 16'd63117; 254: sine = 16'd63922; 255: sine = 16'd64729; 256: sine = 16'd65536; default: sine = 16'd0; endcase end endmodule